【论文阅读】Graph Neural News Recommendation with Unsupervised Preference Disentanglement (ACL 2020)
Task
News Recommendation:给定一系列成对的user-news的数据,表示user之前看过news,预测对于一个未见过的news,user是否会看。
Motivation
之前的做News Recommendation的方法通常的关注点是以下几类:
- 充分利用用户的历史信息,做personalized News Recommendation
- 利用文本内容,得到user和news的好的表示
- 利用外部知识
- 利用topic信息
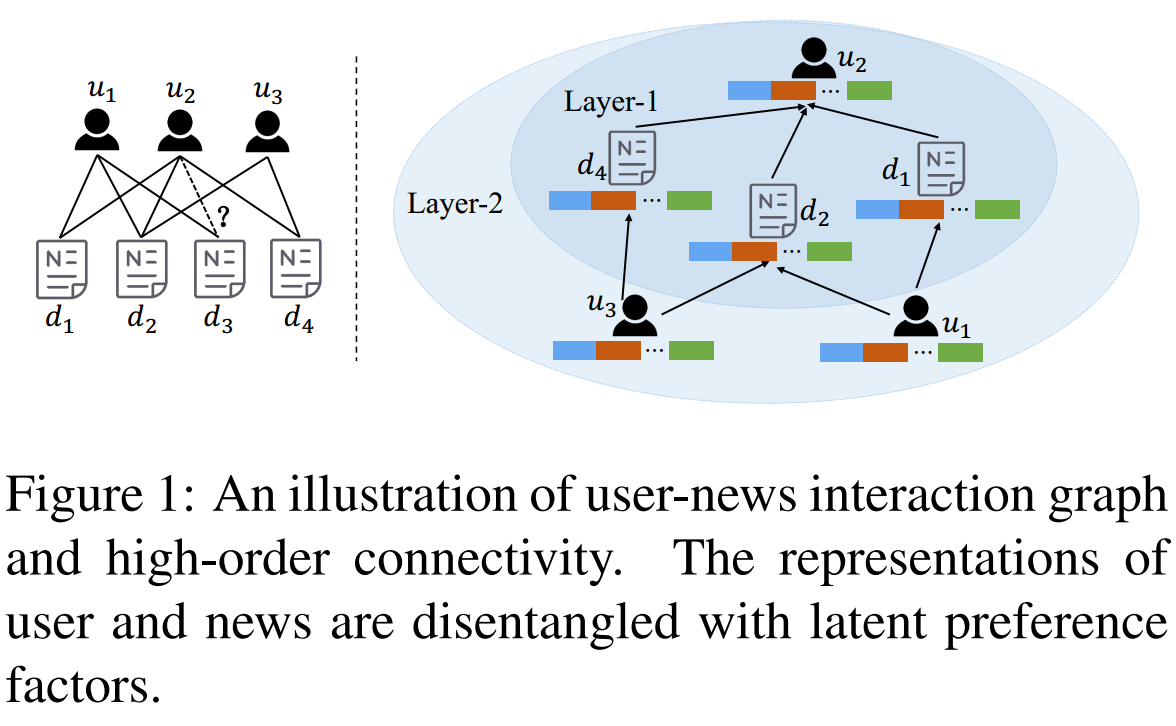
本文方法: - 考虑高阶的user-news之间的关系(News Recommendation中很少)。
- 考虑neighbor对当前的作用时,不应该将所有的neighbor等价看待,而应该给予不同的权重。同时,用户的倾向(preference)具有多样性,可以进一步细分在不同preference下周围neighbor的重要性。所以本文使用了disentangled representations,同时可以增强可解释性。(News Recommendation第一次)
PS:用推荐已经出现了类似的研究(何向南SIGIR2020的DGCF),跟本文很相似。
Method
- 构建二分图:
- 节点:
i. user:随机初始化的向量
ii. news:输入news的title和profile(包括entity和对应的type),使用PCNN分别得到表示,concat作为news的表示。 - 边:user-news之间的click关系,如果一个user点了一个news,则两者之间有一条边。
- 图的更新
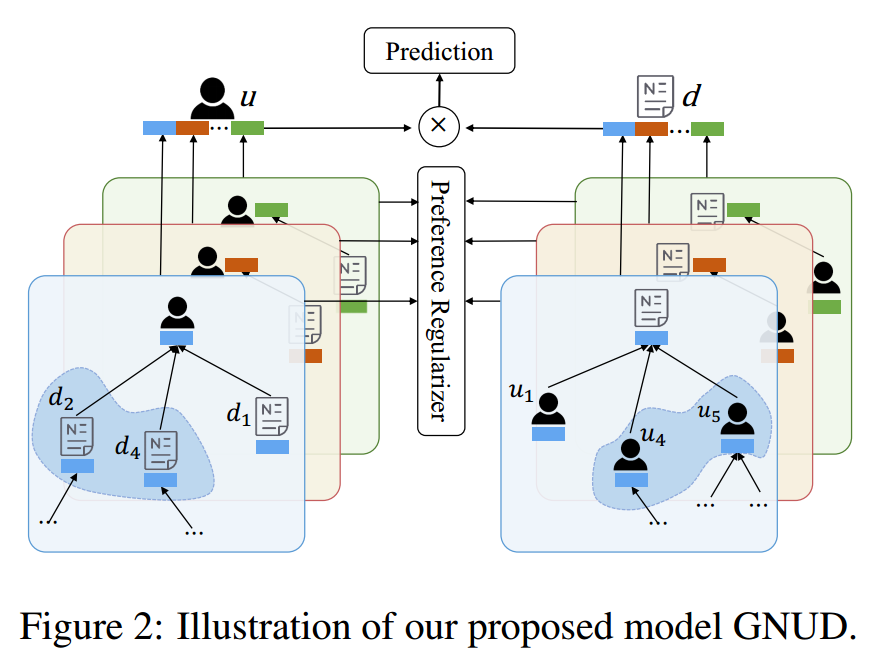
$$y_u = Conv(h_u,{h_d:(u,d)\in \varepsilon })$$
- 维度变换:假定有K个factor,将表示映射到第K个factor的子空间中:
$$s_{i,k} = \frac{ReLU(W_k^Th_i+b_k)}{||ReLU(W_k^Th_i+b_k)||_2}$$ - 表示更新:当更新第k个factor相关的表示时,让与u在第k个factor上相关性高的文本贡献大 - Neighborhood routing algorithm。

$$r^{(t)}_{d,k} = \frac{exp(z^{(t)T}_{u,k}s_{d,k})}{\sum_{k'=1}^{K}{exp(z^{(t)T}_{u,k}s_{d,k})}}$$
$$z^{(t+1)}_{u,k} = \frac{s_{u,k}+\sum_{d:(u,d) \in \varsigma}r^{(t)}_{d,k}s_{d,k})}{||s_{u,k}+\sum_{d:(u,d) \in \varsigma}r^{(t)}_{d,k}s_{d,k})||_2}$$ - 得到最终的表示并计算相似度得到最终的可能性输出:
$$y'_u = W^{(L+1)T}y^{(L)}_u + b^{(L+1)}$$
$$\hat{s}\langle u,d \rangle = y'^T_uy'_d$$
$$\hat{y}_{u,d} = \sigma(\hat{s} \langle u,d \rangle)$$
- Preference Regularizer:为了使得不同的factor得到的表示不同,新增了一个预测任务,即对第k个factor得到的表示进行分类,期望分在第k类的概率最大。
- 模型训练:
- Loss 1: News Recommendation的loss
$$L_1 = -[y_{u,d}ln(\hat{y}_{u,d}) + (1-y_{u,d})ln(1-\hat{y}_{u,d})]$$ - Loss 2: Preference Regularizer的loss
$$L_2 = -\frac{1}{K}\sum_{k=1}^{K}{\sum_{i \in {u,d}}{lnP(k|z_{i,k})[k]}}$$ - 最终的loss:
$$L = \sum_{(u,d) \in T_{train}}{((1-\lambda)L_1 + \lambda L_2) + \eta ||\Theta||}$$
Experiment
- 和SOTA对比
- 消融实验
- 可解释性分析
- 参数分析

 by Mikito
by Mikito