【基础方法】聚类方法（K-means、FCM）

以前通常做的都是分类的问题，虽然说聚类也可以用于分类，但是这方面涉及的比较少，只大概了解了相关的概念。这次简单地介绍学习建模时候看到的三种聚类方法：K-means算法和FCM算法。

K-means聚类方法

K-means聚类方法通过均值进行聚类，每个原始的元素经过聚类后都属于并且只属于某一个类。这是一种严格划分的方法，也可称为硬划分(HCM)。
对于给定的含有$n$个元素的数据集$X$，$x_k$是其中第$k$个元素，$1\leqslant k\leqslant n$。将该数据集聚类为$C$个类，聚类后新的聚类中心集合为$P$，$p_i$是其中第$i$个聚类中心，$1\leqslant k\leqslant C$，则目标函数如下：
$$J_0(X,P)=\sum_{i=1}^{C}\sum_{x_k\in X}(d_{ki})^2$$
其中$d_{ik}$为第$k$个元素和第$i$个聚类中心的失真度，通常用距离表示，如欧氏距离。
算法的具体流程如下：

在数据集$X$中任取$C$个元素，作为初始类别。
通过最近邻方法求出每个元素属于哪一个类，并计算出目标函数$J_0$的值。
计算每一类的均值，作为新的聚类中心。
若$J_0$小于某一个值，或者迭代后新的$J_0$与上一次$J_0$相差小于某个值，则停止；否则转步骤二。

该算法需要预先给定聚类的类别数目，并且受到初始位置的影响。在该算法的基础上，提出了一种二分k-means算法，算法流程如下：

将原数据集先通过k-means分成两类。
将每个类依次再分成两类，并计算出每个类二分时对应的目标函数。
选取最小的目标函数值对应的类，进行二分。
若当前的类别数达到目标类别数，则停止聚类；否则，转到步骤二。

matlab代码

虽然matlab自带kmeans函数，但我还是写了一遍，主要的问题就是生成点了，具体代码如下：

function [U,P] = K_means( X, C )
% 本函数通过K-means方法，将原有数据集聚类，得到C个类。
% 输入：
% X：数据集(n*t)
%    n：数据个数
%    t：数据维数
% C：目标聚类类别数
% 输出：
% U：聚类结果矩阵(n*1)
% P: 聚类中心

% 初始参数设置
[n,~]=size(X);
maxiter=1000;
j0=0;
dvalue=1*10^(-9);
U=zeros(n,1);

% 随机取一些数作为初始聚类中心
ind=randperm(n, C);
P=X(ind,:);

for m=1:maxiter
    j1=0;
    for i=1:n
        d=pdist2(P, X(i,:), 'Euclidean');
        [dist,U(i)]=min(d);
        j1=dist*dist+j1;
    end
    
    if abs(j1-j0)<dvalue
        break
    end
    
    for i=1:C
        P(i,:)=sum(X(U==i,:))/sum(U==i);
    end
    j0=j1;
end

end

主函数：

% % 生成数据
% n=50;
% b=40;
% x(1:n,1:2)=bsxfun(@plus,rand(n,2)*b,[25,25]);
% x(n+1:2*n,1:2)=bsxfun(@plus,rand(n,2)*b,[25,75]);
% x(2*n+1:3*n,1:2)=bsxfun(@plus,rand(n,2)*b,[75,75]);
% x(3*n+1:4*n,1:2)=bsxfun(@plus,rand(n,2)*b,[75,25]);
% save x2.mat x;

% C=4;
% [U, P]=K_means(x,C);
% % 画点
figure;
for i=1:C
    hold on;
    x1=x((U==i),1);
    y1=x((U==i),2);
    scatter(x1,y1);
end

聚类结果如下，对于随机生成的0~100范围内100个点，写的算法分类结果如下：

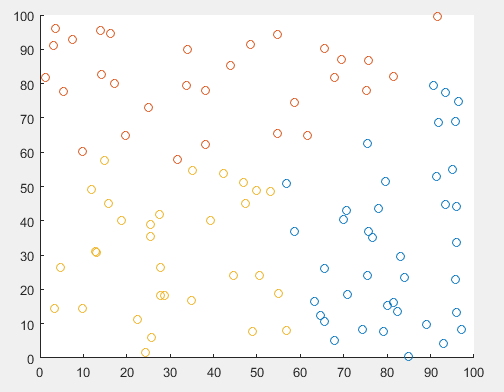
matlab自带的k-means聚类函数聚类结果如下：

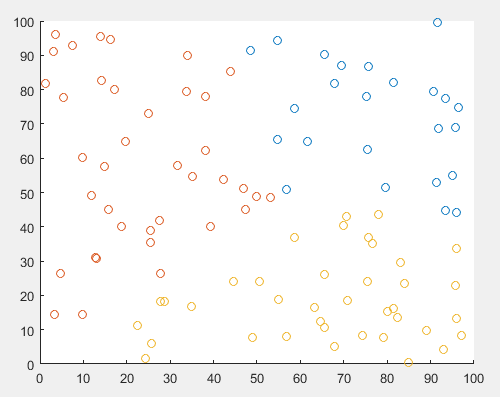
这样的数据点太离散，聚类结果看不出什么，我改变了原始的数据点，聚类结果如下：

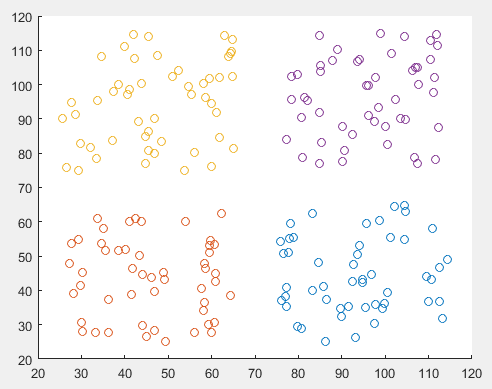
matlab自带的k-means聚类函数聚类结果如下：

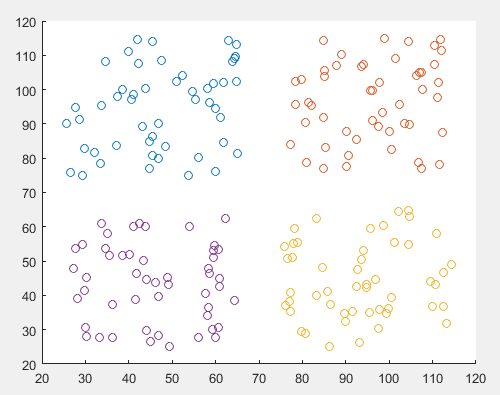
FCM聚类算法

FCM(Fuzzy C-means)算法，也称模糊C均值算法，是一种通过隶属度（每一个元素属于某个类的程度）进行聚类的柔性划分算法。它通过描述每个元素属于某个类的不确定程度进行软聚类。
对于给定的含有$n$个元素的数据集$X$，$x_k$是其中第$k$个元素，$1\leqslant k\leqslant n$。将该数据集聚类为$C$个类，聚类后新的聚类中心集合为$P$，$p_i$是其中第$i$个聚类中心，$1\leqslant k\leqslant C$。
FCM算法通常用一个模糊矩阵描述划分结果。对于K-means聚类方法来说，它的分类矩阵由0和1构成，是一个布尔矩阵。对于FCM算法而言，模糊矩阵 $U=(u_{ki})_{n*c}$ ，其中$0\leqslant u_{ki}\leqslant 1$为隶属度，表示第$k$个元素属于第$i$个类的程度。目标函数如下：
$$J_1(X,P)=\sum_{i=1}^{C}\sum_{x_k\in X}{u_{ki}^m(d_{ki})^2}$$
约束条件：
$$
\forall k, \sum_{i=1}^{C}{u_{ki}}=1
$$
$$
\forall i, \sum_{k=1}^{n}{u_{ki}}>0
$$
其中$m$是加权指数，一般大于1。
使用拉格朗日乘子方法对目标函数求导，得到聚类中心和隶属度计算方法如下：
$$
p_i=\frac{\sum_{j=1}^{n}{u_{ji}^{m}x_j}}{\sum_{j=1}^{n}{u_{ji}^{m}}}
$$
$$
u_{ki}=\frac{1}{\sum_{j=1}^{C}{(\frac{d_ki}{d_kj})^{\frac{2}{m-1}}}}
$$
算法流程如下：

随机初始划分，得到$U$。
得到聚类中心。
计算得到目标函数$J_0$的值。
若$J_0$小于某一个值，或者迭代后新的$J_0$与上一次$J_0$相差小于某个值，则停止；否则更新模糊矩阵，转步骤二。

参考博客：
https://www.cnblogs.com/xiaohuahua108/p/6187178.html
https://blog.csdn.net/taoyanqi8932/article/details/53727841
https://www.cnblogs.com/sddai/p/6259553.html