【基础方法】Harr 小波变换

我在网上了解小波变换的时候，发现它是常用于信号处理的一种方法，但是在论文里也常看到小波变换用于图像处理。小波函数在一定的时间间隔内波形幅度的平均值为0。现在有很多小波函数，Haar小波变换函数是其中最基础的一种，是最简单的正交归一化小波

Harr 简介

我们先看一下Harr相关的函数图形：

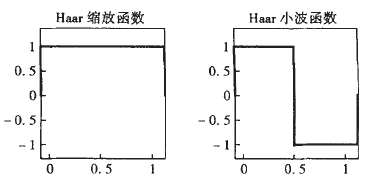
由上图可以以得知Harr小波函数是一个支撑域(函数$\psi(t)$不为0的区间)在$[0,1]$内的单个矩形波，公式如下：
$$\psi(t)=\begin{equation}
\left \{
\begin{aligned}
1 && 0 \leq x < 0.5\\
-1 && 0.5 \leq x \leq 1\\
0 && otherwise\\
\end{aligned}
\right.
\end{equation}$$

算法流程

Haar小波变换步骤

把小波w(t)和原函数f(t)的开始部分进行比较，计算系数C。系数C表示该部分函数与小波的相似程度。
把小波向右移k单位，得到小波w(t-k)，重复1。重复该部知道函数f结束。
扩展小波w(t)，得到小波w(t/2)，重复步骤1,2。
不断扩展小波，重复1,2,3。

假设我们现在有一个一维的表示特征的矩阵$X={x_1,x_2,x_3,x_4}$。
然后对这个一维矩阵进行一次变换：
$$a_{1,0}=\frac{x_1+x_2}{2}$$
$$a_{1,1}=\frac{x_3+x_4}{2}$$
$$d_{1,3}=\frac{x_1-x_2}{2}$$
$$d_{1,4}=\frac{x_3-x_4}{2}$$
这样可以得到一个一维矩阵$Y={a_{1,0},a_{1,1},d_{1,3},d_{1,4}}$。这里的$a_{1,0}$和$a_{1,1}$分别是$x_1,x_2$和$x_3,x_4$的均分，反映了它们的基本特征，所以我们称之为低频成分；而$d_{1,3}$和$d_{1,4}$分别是$x_1,x_2$和$x_3,x_4$的差值，反映了它们的细节信息，所以我们称之为高频成分。
我们也可以再次运用以上的思想对矩阵$Y$再进行一次Haar小波变换，得到最终的小波系数${a_{2,0},d_{2,1},d_{1,3},d_{1,4}}$。

图像处理中的Harr小波变换

对二维图像进行Haar小波变换有两种方法：标准分解和非标准分解。标准分解是指先使用一维小波对图像的每一行的像素值进行变换,产生每一行像素的平均值和细节系数,然后再使用一维小波对这个经过行变换的图像的列进行变换,产生这个图像的平均值和细节系数。非标准分解是指使用一维小波交替地对每一行和每一列像素值进行变换。
对于对图像做小波变换，可以根据自己的需求编写函数，但是matlab也有自带的小波变换函数：dwt2和wavedec2。其中dwt2是二维单尺度小波变换，其可以通过指定小波或者分解滤波器进行二维单尺度小波分解。而wavedec2是二维多尺度小波分解。dwt2的一种语法格式是[cA,cH,cV,cD]=dwt2(X,'wname')；而对应的wavedec的语法格式是[C,S]=wavedec2(X,N,'wname'),其中N为大于1的正整数。也就是说dwt2只能对某个输入矩阵X进行一次分解，而wavedec2可以对输入矩阵X进行N次分解。

matlab示例

Harr小波示例

虽然matlab有自带的小波变换的函数，也可以通过open或者edit打开函数文件，查看源代码，但是忧伤的是，它的源代码往往互相之间都有联系，我打开了也是看不太懂。所以自己写了一个Haar小波的函数，没有做边界处理，就请将就着看看吧。

    function [L,H] = MyHarr( line )
    % line: 一维矩阵，表示一个信号序列，最好行和列都是2的倍数
    % L: 低频成分
    % H: 高频成分
    
    n=length(line);
    n=n/2;
    L=zeros(1, n);
    H=zeros(1,n);
    
    for i=1:n
        L(i)=(line(2*i-1)+line(2*i))/2;
        H(i)=(line(2*i-1)-line(2*i))/2;
    end
    end

matlab的dwt2()函数

dwt2()函数的一般形式就是：

[CA,CH,CV,CD] = dwt2(X,'wname')

CA：approximation coefficients matrix（近似系数矩阵）
CH、CV、CD：details coefficients matrices（细节系数矩阵）

使用并显示的代码如下：

    A=imread('lena.jpg');

    [CA,CH,CV,CD] = dwt2(A,'haar') ;
    subplot(2,2,1);
    imshow(uint8(CA));
    subplot(2,2,2);
    imshow(uint8(CH));
    subplot(2,2,3);
    imshow(uint8(CV));
    subplot(2,2,4);
    imshow(uint8(CD));

显示的效果图为：

matlab的wavedec2()函数

wavedec2()一般使用形式为：

[C,S] = wavedec2(X,N,'wname')

这是一种二维多尺度小波分解函数，分解的次数和传入的参数N有关。其中C是一个行向量，它的组成如下：

C = [ A(N) | H(N) | V(N) | D(N) | ... H(N-1) | V(N-1) | D(N-1) | ... | H(1) | V(1) | D(1) ].

介于这个不太好显示结果，我就不放出matlab代码了，实在需要的话相关的文档中有一段。